What are the steps involved in the key generation process of the RSA cryptosystem, and why is the selection of large prime numbers crucial?

/ / Published in Cybersecurity, EITC/IS/CCF Classical Cryptography Fundamentals, Introduction to public-key cryptography, The RSA cryptosystem and efficient exponentiation, Examination review

The RSA cryptosystem, named after its inventors Rivest, Shamir, and Adleman, is a cornerstone of public-key cryptography. The process of key generation in RSA involves several critical steps, each contributing to the security and functionality of the system. The selection of large prime numbers is fundamental to the strength of RSA encryption, as it directly impacts the difficulty of factorizing the public key, which is the basis of RSA's security.

The key generation process in RSA can be broken down into the following steps:

1. Selection of Two Large Prime Numbers

The first step in RSA key generation is to select two large prime numbers, denoted as p and q. These primes should be chosen randomly and independently of each other. The size of these primes is typically in the range of 2048 to 4096 bits to ensure a high level of security.

Example:
Suppose p = 61 and q = 53. These are relatively small primes for the sake of illustration, but in practice, much larger primes are used.

2. Compute 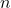n (the Modulus)

Once the primes p and q are selected, the next step is to compute their product, which is denoted as n. The modulus n is a key component of both the public and private keys.

    \[ n = p \times q \]

Example:
For p = 61 and q = 53,

    \[ n = 61 \times 53 = 3233 \]

3. Compute Euler's Totient Function 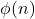\phi(n)

Euler's Totient Function, \phi(n), is calculated using the formula:

    \[ \phi(n) = (p-1) \times (q-1) \]

This function counts the number of integers up to n that are coprime with n.

Example:
For p = 61 and q = 53,

    \[ \phi(n) = (61 - 1) \times (53 - 1) = 60 \times 52 = 3120 \]

4. Choose the Public Exponent e

The public exponent e is selected such that 1 < e < \phi(n) and \gcd(e, \phi(n)) = 1; that is, e must be coprime with \phi(n). Common choices for e include 3, 17, and 65537, as these values balance security and efficiency.

Example:
Let e = 17. Check that \gcd(17, 3120) = 1.

5. Compute the Private Exponent d

The private exponent d is computed as the modular multiplicative inverse of e modulo \phi(n). This means d satisfies the congruence relation:

    \[ d \times e \equiv 1 \ (\text{mod} \ \phi(n)) \]

The Extended Euclidean Algorithm is typically used to find d.

Example:
Using the Extended Euclidean Algorithm, we find d such that:

    \[ 17 \times d \equiv 1 \ (\text{mod} \ 3120) \]

The solution is d = 2753.

6. Form the Public and Private Keys

The public key consists of the pair (e, n), and the private key consists of the pair (d, n).

Example:
Public Key: (17, 3233)
Private Key: (2753, 3233)

Importance of Large Prime Numbers

The security of the RSA cryptosystem relies heavily on the difficulty of factorizing the modulus n back into its prime components p and q. The larger the primes, the more computationally infeasible it becomes for an attacker to perform this factorization using current algorithms and technology.

1. Factorization Difficulty: The primary reason large primes are important is the difficulty of the integer factorization problem. For sufficiently large n, factorizing it into p and q is computationally intensive. The security of RSA is based on the assumption that integer factorization is a hard problem, meaning no efficient (polynomial time) algorithm exists for it.

2. Preventing Attacks: Small primes can be factored relatively quickly using modern algorithms like the General Number Field Sieve (GNFS). By using large primes, the time required to factor n increases exponentially, making brute-force attacks impractical.

3. Ensuring Cryptographic Strength: The length of the keys (2048 bits or more) directly correlates with the cryptographic strength of RSA. Larger key sizes provide a higher level of security, which is necessary to protect against advances in computational power and algorithmic breakthroughs.

4. Prime Generation Algorithms: Efficient algorithms, such as the Miller-Rabin primality test, are used to generate and verify large primes. These algorithms ensure that the primes used in RSA key generation are indeed prime with a high degree of certainty.

Practical Example of RSA Encryption and Decryption

To illustrate the RSA process, consider the following example using the previously generated keys:

Encryption:
To encrypt a plaintext message m (where m is an integer such that 0 \leq m < n), the sender computes the ciphertext c using the recipient's public key (e, n):

    \[ c = m^e \ (\text{mod} \ n) \]

Example:
Let m = 65. Using the public key (17, 3233),

    \[ c = 65^{17} \ (\text{mod} \ 3233) = 2790 \]

Decryption:
To decrypt the ciphertext c, the recipient uses their private key (d, n) to compute the plaintext message m:

    \[ m = c^d \ (\text{mod} \ n) \]

Example:
Using the private key (2753, 3233),

    \[ m = 2790^{2753} \ (\text{mod} \ 3233) = 65 \]

This demonstrates that the original message m is successfully recovered.The RSA key generation process involves the careful selection and computation of large prime numbers, which are fundamental to the security of the cryptosystem. The steps include selecting two large primes, computing their product and totient, choosing a public exponent, calculating the private exponent, and forming the public and private keys. The use of large primes ensures the difficulty of factorizing the modulus, thereby providing robust security against potential attacks.

Other recent questions and answers regarding EITC/IS/CCF Classical Cryptography Fundamentals:

View more questions and answers in EITC/IS/CCF Classical Cryptography Fundamentals

More questions and answers:

Tagged under: , , , , ,