What is the parameter t of the extended eulers algoritm?

/ / Published in Cybersecurity, EITC/IS/CCF Classical Cryptography Fundamentals, Introduction to public-key cryptography, Number theory for PKC – Euclidean Algorithm, Euler’s Phi Function and Euler’s Theorem

The parameter t in the context of the Extended Euclidean Algorithm is a important component used primarily to find the multiplicative inverse of integers in modular arithmetic, which is a foundational concept in public-key cryptography. To understand the role and significance of t, it is essential to consider the mechanics of the Extended Euclidean Algorithm and its applications in number theory and cryptography.

The Euclidean Algorithm

The Euclidean Algorithm is a classical method for computing the greatest common divisor (GCD) of two integers. Given two integers a and b, where a \geq b, the Euclidean Algorithm repeatedly applies the division algorithm to express the GCD as:

    \[ \text{GCD}(a, b) = \text{GCD}(b, a \mod b) \]

This process continues until the remainder is zero. The last non-zero remainder is the GCD of a and b.

The Extended Euclidean Algorithm

The Extended Euclidean Algorithm extends the basic Euclidean Algorithm to not only find the GCD of two integers a and b but also to express this GCD as a linear combination of a and b. Specifically, it finds integers x and y such that:

    \[ \text{GCD}(a, b) = ax + by \]

These integers x and y are known as the Bézout coefficients. The algorithm proceeds by maintaining and updating these coefficients through each step of the Euclidean Algorithm.

Parameter 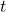t in the Extended Euclidean Algorithm

To illustrate the significance of t, let's consider the steps of the Extended Euclidean Algorithm in more detail. Suppose we are given two integers a and b with a \geq b.

1. Initialization: Start with a and b. Initialize the coefficients:

    \[ x_0 = 1, \quad y_0 = 0, \quad x_1 = 0, \quad y_1 = 1 \]

2. Iteration: For each step i, compute the quotient and remainder:

    \[ q_i = \left\lfloor \frac{a_i}{b_i} \right\rfloor, \quad r_i = a_i \mod b_i \]

Update a and b:

    \[ a_{i+1} = b_i, \quad b_{i+1} = r_i \]

Update the coefficients:

    \[ x_{i+1} = x_{i-1} - q_i x_i, \quad y_{i+1} = y_{i-1} - q_i y_i \]

3. Termination: The algorithm terminates when b_i = 0. At this point, a_i is the GCD of the original a and b, and x_i and y_i are the Bézout coefficients.

Example

Consider finding the GCD of 240 and 46, and expressing it as a linear combination.

1. Initialization:

    \[ a = 240, \quad b = 46 \]

    \[ x_0 = 1, \quad y_0 = 0, \quad x_1 = 0, \quad y_1 = 1 \]

2. First Iteration:

    \[ q_1 = \left\lfloor \frac{240}{46} \right\rfloor = 5, \quad r_1 = 240 \mod 46 = 10 \]

    \[ a_1 = 46, \quad b_1 = 10 \]

    \[ x_2 = x_0 - q_1 x_1 = 1 - 5 \cdot 0 = 1, \quad y_2 = y_0 - q_1 y_1 = 0 - 5 \cdot 1 = -5 \]

3. Second Iteration:

    \[ q_2 = \left\lfloor \frac{46}{10} \right\rfloor = 4, \quad r_2 = 46 \mod 10 = 6 \]

    \[ a_2 = 10, \quad b_2 = 6 \]

    \[ x_3 = x_1 - q_2 x_2 = 0 - 4 \cdot 1 = -4, \quad y_3 = y_1 - q_2 y_2 = 1 - 4 \cdot (-5) = 21 \]

4. Third Iteration:

    \[ q_3 = \left\lfloor \frac{10}{6} \right\rfloor = 1, \quad r_3 = 10 \mod 6 = 4 \]

    \[ a_3 = 6, \quad b_3 = 4 \]

    \[ x_4 = x_2 - q_3 x_3 = 1 - 1 \cdot (-4) = 5, \quad y_4 = y_2 - q_3 y_3 = -5 - 1 \cdot 21 = -26 \]

5. Fourth Iteration:

    \[ q_4 = \left\lfloor \frac{6}{4} \right\rfloor = 1, \quad r_4 = 6 \mod 4 = 2 \]

    \[ a_4 = 4, \quad b_4 = 2 \]

    \[ x_5 = x_3 - q_4 x_4 = -4 - 1 \cdot 5 = -9, \quad y_5 = y_3 - q_4 y_4 = 21 - 1 \cdot (-26) = 47 \]

6. Fifth Iteration:

    \[ q_5 = \left\lfloor \frac{4}{2} \right\rfloor = 2, \quad r_5 = 4 \mod 2 = 0 \]

    \[ a_5 = 2, \quad b_5 = 0 \]

    \[ x_6 = x_4 - q_5 x_5 = 5 - 2 \cdot (-9) = 23, \quad y_6 = y_4 - q_5 y_5 = -26 - 2 \cdot 47 = -120 \]

The algorithm terminates at this point, with a_5 = 2 being the GCD of 240 and 46. The Bézout coefficients are x_5 = -9 and y_5 = 47, giving us the equation:

    \[ 2 = 240 \cdot (-9) + 46 \cdot 47 \]

Application in Cryptography

In the realm of public-key cryptography, particularly within the RSA algorithm, the Extended Euclidean Algorithm is employed to find the modular inverse. Given an integer e (the public exponent) and \phi(n) (Euler's totient function of n), the goal is to find an integer d (the private exponent) such that:

    \[ ed \equiv 1 \pmod{\phi(n)} \]

This is equivalent to finding d such that:

    \[ ed - k\phi(n) = 1 \]

for some integer k. Here, d is the multiplicative inverse of e modulo \phi(n). The Extended Euclidean Algorithm is used to compute this d.

The parameter t in the Extended Euclidean Algorithm is essentially the quotient q_i at each step of the algorithm. These quotients are used to iteratively update the coefficients x and y until the GCD is found. The Extended Euclidean Algorithm's ability to find these coefficients is what makes it invaluable in cryptographic applications, particularly in finding modular inverses which are important for key generation and encryption/decryption processes in public-key cryptography.

Other recent questions and answers regarding EITC/IS/CCF Classical Cryptography Fundamentals:

View more questions and answers in EITC/IS/CCF Classical Cryptography Fundamentals

More questions and answers:

Tagged under: , , , , ,