Why is it necessary for the key (A) in the Affine Cipher to be coprime with the modulus 26, and what are the implications if it is not?

/ / Published in Cybersecurity, EITC/IS/CCF Classical Cryptography Fundamentals, History of cryptography, Modular arithmetic and historical ciphers, Examination review

The Affine Cipher is a type of monoalphabetic substitution cipher that utilizes mathematical operations to encrypt and decrypt messages. The encryption process in the Affine Cipher involves two keys, typically denoted as A and B, and follows the formula:

    \[ E(x) = (Ax + B) \mod 26 \]

where E(x) represents the encrypted letter, x is the numerical equivalent of the plaintext letter (with a = 0, b = 1, \ldots, z = 25), A and B are keys, and 26 is the modulus, corresponding to the number of letters in the English alphabet.

For decryption, the formula used is:

    \[ D(y) = A^{-1}(y - B) \mod 26 \]

where D(y) represents the decrypted letter, y is the numerical equivalent of the ciphertext letter, and A^{-1} is the modular multiplicative inverse of A modulo 26.

The necessity for the key A to be coprime with the modulus 26 stems from the requirement to find the modular multiplicative inverse of A during the decryption process. A number A is said to be coprime (or relatively prime) with another number n if their greatest common divisor (GCD) is 1, i.e., \text{GCD}(A, n) = 1.

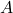Why Key A Must Be Coprime with 26

1. Existence of Modular Inverse:
The modular multiplicative inverse of A modulo 26 exists if and only if A and 26 are coprime. The modular inverse A^{-1} is a number such that:

    \[ A \cdot A^{-1} \equiv 1 \mod 26 \]

If A is not coprime with 26, the equation above has no solution, meaning A^{-1} does not exist. Without the inverse, the decryption formula cannot be applied, rendering the decryption process infeasible.

2. Ensuring Unique Decryption:
When A and 26 are coprime, each ciphertext letter maps uniquely to one plaintext letter. If A is not coprime with 26, the mapping between plaintext and ciphertext is not bijective, leading to multiple plaintext letters potentially mapping to the same ciphertext letter. This ambiguity undermines the cipher's reliability and security.

3. Mathematical Properties:
The coprimality condition ensures that the linear transformation applied by the Affine Cipher is invertible. The mathematical foundation of the Affine Cipher relies on linear algebra principles, where invertibility is important for reversing the transformation.

Implications if 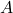A is not Coprime with 26

1. Non-existence of Inverse:
If A is not coprime with 26, the modular inverse A^{-1} does not exist. For example, if A = 13, which shares a common factor of 13 with 26, there is no integer A^{-1} such that:

    \[ 13 \cdot A^{-1} \equiv 1 \mod 26 \]

Consequently, it is impossible to decrypt the ciphertext using the standard decryption formula.

2. Ambiguity in Decryption:
Suppose A = 2, which is not coprime with 26 (since \text{GCD}(2, 26) = 2). In this case, the mapping is not one-to-one. For instance, both plaintext letters 'a' (x = 0) and 'n' (x = 13) would map to the same ciphertext letter:

    \[ E(0) = (2 \cdot 0 + B) \mod 26 = B \mod 26 \]

    \[ E(13) = (2 \cdot 13 + B) \mod 26 = (26 + B) \mod 26 = B \mod 26 \]

This results in a ciphertext where multiple plaintext letters correspond to the same ciphertext letter, creating ambiguity and making it impossible to uniquely determine the original plaintext.

3. Security Weakness:
The security of the Affine Cipher relies on the difficulty of deducing the keys from the ciphertext. If A is not coprime with 26, the cipher becomes more predictable and easier to break. The redundancy introduced by non-coprime A values reduces the effective key space, making the cipher more vulnerable to cryptanalysis.

Example of Valid and Invalid Keys

– Valid Key Example:
Let A = 5 and B = 8.

Since \text{GCD}(5, 26) = 1, A is coprime with 26. The encryption function is:

    \[ E(x) = (5x + 8) \mod 26 \]

To decrypt, we need the modular inverse of 5 modulo 26. Using the Extended Euclidean Algorithm, we find that 5^{-1} \equiv 21 \mod 26. The decryption function is:

    \[ D(y) = 21(y - 8) \mod 26 \]

This ensures that each ciphertext letter can be uniquely decrypted to its corresponding plaintext letter.

– Invalid Key Example:
Let A = 6 and B = 3.

Since \text{GCD}(6, 26) = 2, A is not coprime with 26. The encryption function is:

    \[ E(x) = (6x + 3) \mod 26 \]

Attempting to decrypt, we find that 6 does not have a modular inverse modulo 26. Therefore, the decryption process cannot be performed using the standard formula, leading to an unusable cipher.

Conclusion

The requirement for the key A in the Affine Cipher to be coprime with the modulus 26 is fundamental to the cipher's functionality. It ensures the existence of a modular inverse, which is essential for the decryption process. Without this condition, the cipher fails to provide a unique and reversible mapping between plaintext and ciphertext, compromising both the usability and security of the encryption scheme.

Other recent questions and answers regarding EITC/IS/CCF Classical Cryptography Fundamentals:

View more questions and answers in EITC/IS/CCF Classical Cryptography Fundamentals

More questions and answers:

Tagged under: , , , , ,