What is the significance of the group ( (mathbb{Z}/pmathbb{Z})^* ) in the context of the Diffie-Hellman key exchange, and how does group theory underpin the security of the protocol?
The group ![]() plays a pivotal role in the Diffie-Hellman key exchange protocol, a cornerstone of modern cryptographic systems. To understand its significance, one must consider the structure of this group and the mathematical foundations that ensure the security of the Diffie-Hellman protocol.
plays a pivotal role in the Diffie-Hellman key exchange protocol, a cornerstone of modern cryptographic systems. To understand its significance, one must consider the structure of this group and the mathematical foundations that ensure the security of the Diffie-Hellman protocol.
The Group 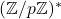
The notation ![]() refers to the multiplicative group of integers modulo
refers to the multiplicative group of integers modulo ![]() , where
, where ![]() is a prime number. This group consists of all integers from 1 to
is a prime number. This group consists of all integers from 1 to ![]() that are coprime to
that are coprime to ![]() (which, for a prime
(which, for a prime ![]() , is every integer from 1 to
, is every integer from 1 to ![]() ). The operations within this group are performed modulo
). The operations within this group are performed modulo ![]() .
.
Mathematically, ![]() is defined as:
is defined as:
![]()
Since ![]() is prime, every non-zero element in
is prime, every non-zero element in ![]() has a multiplicative inverse, making
has a multiplicative inverse, making ![]() a cyclic group of order
a cyclic group of order ![]() . The cyclic nature of this group means that there exists a generator
. The cyclic nature of this group means that there exists a generator ![]() such that every element of the group can be expressed as a power of
such that every element of the group can be expressed as a power of ![]() .
.
Diffie-Hellman Key Exchange Protocol
The Diffie-Hellman key exchange is a method that allows two parties to securely share a common secret over an insecure channel. The protocol leverages the properties of ![]() to achieve this goal. The steps involved in the Diffie-Hellman key exchange are as follows:
to achieve this goal. The steps involved in the Diffie-Hellman key exchange are as follows:
1. Public Parameters: Both parties agree on a large prime ![]() and a generator
and a generator ![]() of the group
of the group ![]() .
.
2. Private Keys: Each party selects a private key. Let's denote Alice's private key as ![]() and Bob's private key as
and Bob's private key as ![]() , where
, where ![]() .
.
3. Public Keys: Each party computes their public key by raising the generator ![]() to the power of their private key, modulo
to the power of their private key, modulo ![]() . Thus, Alice computes
. Thus, Alice computes ![]() and Bob computes
and Bob computes ![]() .
.
4. Exchange: Alice and Bob exchange their public keys ![]() and
and ![]() over the insecure channel.
over the insecure channel.
5. Shared Secret: Each party computes the shared secret by raising the received public key to the power of their private key. Alice computes ![]() and Bob computes
and Bob computes ![]() . Due to the properties of exponentiation in modular arithmetic, both computations yield the same result:
. Due to the properties of exponentiation in modular arithmetic, both computations yield the same result:
![]()
This shared secret ![]() can then be used as a key for subsequent symmetric encryption.
can then be used as a key for subsequent symmetric encryption.
Security of the Diffie-Hellman Protocol
The security of the Diffie-Hellman key exchange relies on the difficulty of the Discrete Logarithm Problem (DLP) in the group ![]() . The DLP can be stated as follows: given a prime
. The DLP can be stated as follows: given a prime ![]() , a generator
, a generator ![]() of
of ![]() , and an element
, and an element ![]() in the group, find the integer
in the group, find the integer ![]() such that:
such that:
![]()
This problem is believed to be computationally infeasible for large primes ![]() , which underpins the security of the Diffie-Hellman protocol. An attacker who intercepts the public keys
, which underpins the security of the Diffie-Hellman protocol. An attacker who intercepts the public keys ![]() and
and ![]() would need to solve the DLP to determine the shared secret
would need to solve the DLP to determine the shared secret ![]() , which is considered impractical for appropriately chosen parameters.
, which is considered impractical for appropriately chosen parameters.
Mathematical Underpinnings
The security of the Diffie-Hellman protocol is deeply rooted in group theory and number theory. The key aspects include:
1. Cyclic Groups: The group ![]() is cyclic, meaning it can be generated by a single element
is cyclic, meaning it can be generated by a single element ![]() . This property ensures that the exponentiation operation used in the protocol covers all possible non-zero elements of the group, maximizing the difficulty of the DLP.
. This property ensures that the exponentiation operation used in the protocol covers all possible non-zero elements of the group, maximizing the difficulty of the DLP.
2. Modular Arithmetic: The use of modular arithmetic ensures that the computations remain within a fixed range, preventing overflow and ensuring efficient computation. The modular nature also contributes to the one-way function property of exponentiation, where computing ![]() is straightforward, but finding
is straightforward, but finding ![]() given
given ![]() and
and ![]() is difficult.
is difficult.
3. Hardness Assumptions: The security relies on the assumption that solving the DLP in ![]() is hard. This assumption is supported by the lack of efficient algorithms for the DLP in general, despite significant research efforts in computational number theory.
is hard. This assumption is supported by the lack of efficient algorithms for the DLP in general, despite significant research efforts in computational number theory.
Example
Consider a simple example with small numbers for illustrative purposes. Let ![]() and
and ![]() , which is a generator of
, which is a generator of ![]() .
.
1. Alice chooses a private key ![]() and computes her public key:
and computes her public key:
![]()
2. Bob chooses a private key ![]() and computes his public key:
and computes his public key:
![]()
3. Alice and Bob exchange their public keys ![]() and
and ![]() .
.
4. Alice computes the shared secret using Bob's public key:
![]()
5. Bob computes the shared secret using Alice's public key:
![]()
Both Alice and Bob obtain the same shared secret ![]() , which can be used for secure communication.The group
, which can be used for secure communication.The group ![]() is integral to the Diffie-Hellman key exchange due to its cyclic nature and the computational hardness of the Discrete Logarithm Problem within this group. The protocol's security is underpinned by these mathematical properties, ensuring that an adversary cannot feasibly determine the shared secret without solving the DLP. This makes the Diffie-Hellman key exchange a robust method for secure key exchange in cryptographic systems.
is integral to the Diffie-Hellman key exchange due to its cyclic nature and the computational hardness of the Discrete Logarithm Problem within this group. The protocol's security is underpinned by these mathematical properties, ensuring that an adversary cannot feasibly determine the shared secret without solving the DLP. This makes the Diffie-Hellman key exchange a robust method for secure key exchange in cryptographic systems.
Other recent questions and answers regarding Diffie-Hellman cryptosystem:
- In the context of elliptic curve cryptography (ECC), how does the elliptic curve discrete logarithm problem (ECDLP) compare to the classical discrete logarithm problem in terms of security and efficiency, and why are elliptic curves preferred in modern cryptographic applications?
- How do square root attacks, such as the Baby Step-Giant Step algorithm and Pollard's Rho method, affect the required bit lengths for secure parameters in cryptographic systems based on the discrete logarithm problem?
- Why is the security of the Diffie-Hellman cryptosystem considered to be dependent on the computational difficulty of the discrete logarithm problem, and what are the implications of potential advancements in solving this problem?
- What are the primary differences between the classical discrete logarithm problem and the generalized discrete logarithm problem, and how do these differences impact the security of cryptographic systems?
- How does the Diffie-Hellman key exchange protocol ensure that two parties can establish a shared secret over an insecure channel, and what is the role of the discrete logarithm problem in this process?
- Why are larger key sizes (e.g., 1024 to 2048 bits) necessary for the security of the Diffie-Hellman cryptosystem, particularly in the context of index calculus attacks?
- What are square root attacks, such as the Baby Step-Giant Step algorithm and Pollard's Rho method, and how do they impact the security of Diffie-Hellman cryptosystems?
- What is the Generalized Discrete Logarithm Problem (GDLP) and how does it extend the traditional Discrete Logarithm Problem?
- How does the security of the Diffie-Hellman cryptosystem rely on the difficulty of the Discrete Logarithm Problem (DLP)?
- What is the Diffie-Hellman key exchange protocol and how does it ensure secure key exchange over an insecure channel?
View more questions and answers in Diffie-Hellman cryptosystem

